Inequações do 2º grau

As inequações são expressões matemáticas que utilizam, na sua formatação, os seguintes sinais de desigualdades:

>: maior que
<: menor que
≥: maior ou igual
≤: menor ou igual
≠: diferente

As inequações do 2º grau são resolvidas utilizando o teorema de Bháskara. O resultado deve ser comparado ao sinal da inequação, com o objetivo de formular o conjunto solução.

Exemplo 1
Vamos resolver a inequação 3x² + 10x + 7 < 0.

S = {x ? R / –7/3 < x < –1}

Regrinhas:
1° Realizar um estudo do sinal da função y= ax² + bx +c.
2° Determinar os valores de x que atendam à desigualdade da inequação.

Por Marcos Noé
Graduado em Matemática

Estudo do sinal de uma função quadrática

Regrinhas:

1° Calcular o(s) zero(s) da função.

OBS: O(s) zero(s) da função são os valores de “x” que tornaram a função NULA.
2°  Para verificar os valores de “x” que tornam a função positiva ou negativa, basta pegar o antecessor e o sucessor do(s) o(s) zero(s) da função e substituir em “x“ pra verificar se a função é positiva, negativa ou nula, conforme foi realizado no exemplo em sala de aula e que vocês copiaram no caderno.

3° Após a substituição, deve-se escrever os valores de “x” que tornam a função positiva, negativa ou nula.

Observação importante!

Y > 0 – Função POSITIVA.
Y < 0 – Função NEGATIVA.
Y = 0 – Função NULA

Valor máximo e mínimo da função quadrática

Considere uma função do 2º grau qualquer, do tipo f(x) = ax² + bx + c, com a ≠ 0. Sabemos que seu gráfico é uma parábola e que a concavidade da parábola varia de acordo com o coeficiente a. Ou seja:
Se a < 0 → a concavidade da parábola é voltada para baixo; 
Se a > 0 → a concavidade da parábola é voltada para cima; 

Sabemos também que o valor de Δ = b² – 4ac determina quantos pontos a parábola intercepta o eixo x. Ou seja:
Δ > 0 → a função tem duas raízes reais, logo intercepta o eixo x em dois pontos; 
Δ < 0 → a função não possui raízes reais, logo não intercepta o eixo x; 
Δ = 0 → a função possui apenas uma raiz real, logo intercepta o eixo x em apenas um ponto; 

Vimos anteriormente que o vértice da parábola pode ser um ponto de mínimo absoluto ou de máximo absoluto, e o que determina um caso ou outro é a concavidade da parábola. 

Se a concavidade for voltada para baixo, a função apresenta ponto de máximo absoluto. 
Se a concavidade for voltada para cima, a função apresenta ponto de mínimo absoluto. 

As coordenadas do vértice da parábola são dadas por: 

Exemplo 1: Dadas as funções abaixo, determine se elas possuem ponto de máximo ou mínimo absoluto e as coordenadas desses pontos. 

a) f(x) = 3x² – 4x + 1 

Solução: Observando a função, podemos afirmar que a = 3 > 0. Portanto, o gráfico da função é uma parábola com a concavidade voltada para cima. Isso implica que a função apresenta um ponto de mínimo absoluto. Vimos que esse ponto é o vértice da parábola e para determinar suas coordenadas utilizamos as fórmulas: 

 Dessa forma, o ponto de máximo absoluto, que é o vértice da parábola, tem coordenadas:

Por Marcelo Rigonatto
Especialista em Estatística e Modelagem Matemática

Coordenadas do vértice

Para determinarmos os vértices de uma parábola temos que encontrar o par ordenado de pontos que constituem as coordenadas de retorno da parábola. Esse ponto de retorno da parábola, mais conhecido como vértice da parábola, pode ser calculado com base nas expressões matemáticas envolvendo os coeficientes da função do 2º grau dada pela lei de formação y = ax² + bx + c. 

O valor de x na determinação do vértice de uma parábola é dado por  e o valor de y é calculado por  . Nesse caso, temos que, quando o coeficiente a for maior que zero, a parábola possui valor mínimo e quando a menor que zero, valor máximo. 


Valor mínimo (a > 0)

Valor máximo (a < 0) 

Exemplo 
Para produzirmos x unidades de uma mercadoria, temos que o custo dessa produção em reais é dado pela expressão matemática C = x² – 80x + 3000. Com base nessa expressão, determine a quantidade de unidades produzidas para que o custo seja mínimo e qual o valor mínimo do custo. 

Quantidade de unidades produzidas para que o custo seja mínimo será de 40 peças. 

Observe:

Valor mínimo do custo será de R$ 1 400,00. 

Veja:

Por Marcos Noé
Graduado em Matemática

Função quadrática

 Definição

Chama-se função quadrática, ou função polinomial do 2º grau, qualquer função f de IR em IR dada por uma lei da forma f(x) = ax² + bx + c, onde a, b e c são números reais e a 0.

Vejamos alguns exemplos de função quadráticas:

1. f(x) = 3x² - 4x  + 1, onde a = 3, b = - 4 e c = 1
2. f(x) = x² -1, onde a = 1, b = 0 e c = -1
3. f(x) = 2x² + 3x + 5, onde a = 2, b = 3 e c = 5
4. f(x) = - x² + 8x, onde a = -1, b = 8 e c = 0
5. f(x) = -4x², onde a = - 4, b = 0 e c = 0

 Gráfico

O gráfico de uma função polinomial do 2º grau, y = ax² + bx + c, com a 0, é uma curva chamada parábola.

Exemplo:

Vamos construir o gráfico da função y = x² + x:

Primeiro atribuímos a x alguns valores, depois calculamos o valor correspondente de y e, em seguida, ligamos os pontos assim obtidos.

x y -3 6 -2 2 -1 0 0 0 1 2 2 6

Observação:

Ao construir o gráfico de uma função quadrática y = ax² + bx + c, notaremos sempre que:

• se   a > 0, a parábola tem a concavidade voltada para cima;
• se   a < 0, a parábola tem a concavidade voltada para baixo;

Zero e Equação do 2º Grau

    Chama-se zeros ou raízes da função polinomial do 2º grau f(x) = ax² + bx + c , a 0, os números reais x tais que f(x) = 0.

    Então as raízes da função f(x) = ax² + bx + c são as soluções da equação do 2º grau ax² + bx + c = 0, as quais são dadas pela chamada fórmula de Bhaskara:

  

Temos:

                    

Observação

A quantidade de raízes reais de uma função quadrática depende do valor obtido para o radicando ,  chamado discriminante, a saber:

• quando  é positivo, há duas raízes reais e distintas;
• quando  é zero, há só uma raiz real (para ser mais preciso, há duas raízes iguais);
• quando  é negativo, não há raiz real.

Inequação do 1° grau

Uma inequação do 1° grau na incógnita x é qualquer expressão do 1° grau que pode ser escrita numa das seguintes formas:

ax + b > 0;
ax + b < 0;
ax + b ≥ 0;
ax + b ≤ 0.

Onde a, b são números reais com a ≠ 0.

Exemplos:

-2x + 7 > 0
x – 10 ≤ 0
2x + 5 ≤ 0
12 – x < 0

Resolvendo uma inequação de 1° grau

Uma maneira simples de resolver uma equação do 1° grau é isolarmos a incógnita x em um dos membros da igualdade. Observe dois exemplos:

Exemplo1: Resolva a inequação -2x + 7 > 0.

Solução:

-2x > -7

Multiplicando por (-1)

2x < 7
x < 7/2

Portanto a solução da inequação é x < 7/2.

Exemplo 2: Resolva a inequação 2x – 6 < 0.

Solução:
2x < 6
x < 6/2
x < 3

Portanto a solução da inequação e x < 3

Pode-se resolver qualquer inequação do 1° grau por meio do estudo do sinal de uma função do 1° grau, com o seguinte procedimento:

1. Iguala-se a expressão ax + b a zero;
2. Localiza-se a raiz no eixo x;
3. Estuda-se o sinal conforme o caso.

Exemplo 1:

-2x + 7 > 0
-2x + 7 = 0
x = 7/2

Exemplo 2:

2x – 6 < 0
2x – 6 = 0
x = 3

Zero da função, variação da função e estudo do sinal

Zero da Função

Denominamos zero da função o valor de x para o qual a função de x é igual a zero, ou seja, o valor de x que faz com que y seja igual a zero.

Exemplo:

Determine o zero da função definida por y = 2x - 2:

2x - 2 = 0

2x = 2

x = 2/2

x = 1

Variação da função 

Se em em uma função, aumentando o valor para x, o valor da função aumenta, temos então uma função crescente. Mas, se aumentando o valor para x, o valor da função diminui, temos uma função decrescente.

Quando a > 0 a função será crescente.

Quando a < 0 a função será decrescente.

Quando a = 0 a função será constante.

   

Estudo do sinal da Função

Em uma função, podemos determinar os valores reais de x que a tornam positiva, negativa ou nula.

Quando y = 0 a função será nula.

Quando y > 0 a função será positiva.

Quando y < 0 a função será negativa.

   

Representação grafica da função afim

Regrinhas:
1° Atribuir valores aleatórios à incógnita x.
2° Determinar os valores de y correspondentes aos valores de x utilizados.
3° Indicar no plano cartesiano os pontos encontrados.
4° Unir esses pontos.

Função afim, linear e constante

Função afim

Uma função definida por f: R→R chama-se afim quando existem constantes a, b que pertencem ao conjunto dos reais tais que f(x)= ax + b para todo x ∈ R. A lei que define função afim é:

Função linear

Uma função definida por f: R→R chama-se linear quando existe uma constante a ∈ R tal que f(x) = ax para todo x ∈ R. A lei que define uma função linear é a seguinte:

Função constante

Uma função definida por f: R→R chama-se constante quando existe uma constante b R tal que f(x) = b para todo x ∈ R. A lei que define uma função constante é:

Funções

As funções nada mais são que um tipo particular de relação que possuem uma propriedade específica.

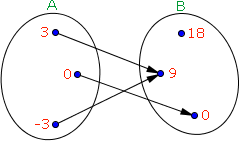
Para iniciarmos o estudo das funções vamos começar analisando a relação 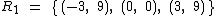, cujo diagrama de flechas pode ser visto ao lado:

Observe que todos os elementos do conjunto A possuem uma flecha em direção a um único elemento do conjunto B.

Em outras palavras, não há no conjunto A qualquer elemento que não esteja associado a um elemento do conjunto B e os elementos de A estão associados a apenas um elemento de B.

Por possuir tal propriedade, dizemos que esta relação é uma função f de A em B representada por:

Domínio da Função

Ao conjunto A damos o nome de domínio da função.

O domínio é o conjunto de partida. Ele composto de todos os elementos do conjunto de partida.

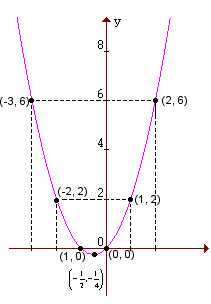
Neste nosso exemplo o domínio da função f é representado por D = { -3, 0, 3 }, ou seja, o domínio desta função contém todos os elementos do conjunto A.

Como supracitado, para que tenhamos uma função, todos os elementos do domínio devem estar associados a um e somente um dos elementos de B.

Contradomínio da Função

Ao conjunto B damos o nome de contradomínio da função.

O contradomínio é o conjunto de chegada. Ele composto de todos os elementos do conjunto de chegada.

Em nosso exemplo o contradomínio da função f é representado por CD = { 0, 9, 18 }, isto é, o contradomínio desta função contém todos os elementos do conjunto B.

Segundo o conceito de função não é necessário que todos os elementos de B estejam relacionados aos elementos do domínio. Note que no conjunto B o elemento 18 não recebe nenhuma flecha, isto é, não está relacionado a qualquer elemento de A.

Uma outra coisa que deve ser observada é que em uma função os elementos do contradomínio podem receber mais de uma flechada, se associando, portanto, a mais de um elemento do domínio. Como exemplo temos o elemento 9 que está associado aos elementos do domínio -3 e 3.

Imagem da Função

A imagem da função dependendo do caso é o próprio contradomínio, ou então é um subconjunto seu.

Os elementos do conjunto imagem são todos os elementos do contradomínio que estão associados a algum elemento do domínio. No exemplo que estamos utilizando o conjunto imagem é representado por Im  = { 0, 9 }, pois 0 e 9 são todos os elementos do CD que estão associados a algum elemento do D.

Em resumo para a função de exemplo temos:

Domínio da Função: D = { -3, 0, 3 }

Contradomínio da Função: CD  = { 0, 9, 18 }

Conjunto Imagem da Função: Im = { 0, 9 }

Nesta função exemplo o conjunto imagem é um subconjunto do contradomínio, pois o elemento 18 de B não está contido no conjunto imagem, por não estar associado a nenhum elemento do domínio.

Exemplos de Relação que não é Função

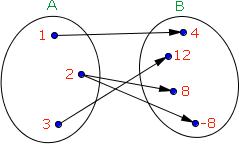
Observe o diagrama de flechas ao lado:

Ele não representa uma função de A em B, pois o elemento 2 do conjunto A possui duas imagens, -8 e 8, o que contraria o conceito de função.

Se apenas 8 ou -8 recebessem um flechada de 2, aí sim teríamos uma função.

Problemas envolvendo equações do 2° grau

• Determine dois números inteiros consecutivos tais que a soma de seus inversos seja 13/42.

1/x + 1/y = 13/42

42(x + 1)/42x(x + 1) + 42x/42x(x+1) = 13x(x +1)/42x(x + 1)

42x(x + 1) + 42x = 13x • (x + 1)
42x + 42 +42x = 13x² - 13x

13y² - 71x -42 = 0

Resolvendo obtemos: x¹ = 6 e x² = -7/13
A raiz -7/13 não é utilizada, pois não se trata de número inteiro. Portanto, os números pedidos são 6 e o seu consecutivo 7.  

Sistemas de equações do 2° grau

Exemplo 1

Isolando x ou y na 2ª equação do sistema: 

x + y = 6 
x = 6 – y 

Substituindo o valor de x na 1ª equação: 

x² + y² = 20 
(6 – y)² + y² = 20 
(6)² – 2 * 6 * y + (y)² + y² = 20 
36 – 12y + y² + y² – 20 = 0 
16 – 12y + 2y² = 0 
2y² – 12y + 16 = 0 (dividir todos os membros da equação por 2) 

y² – 6y + 8 = 0 

∆ = b² – 4ac 
∆ = (–6)² – 4 * 1 * 8 
∆ = 36 – 32 
∆ = 4 

a = 1, b = –6 e c = 8

Determinando os valores de x em relação aos valores de y obtidos: 

Para y = 4, temos: 
x = 6 – y 
x = 6 – 4 
x = 2 

Par ordenado (2; 4) 


Para y = 2, temos: 
x = 6 – y 
x = 6 – 2 
x = 4 

Par ordenado (4; 2) 

S = {(2: 4) e (4; 2)} 

Exemplo 2

Isolando x ou y na 2ª equação: 
x – y = –3 
x = y – 3 

Substituindo o valor de x na 1ª equação: 

x² + 2y² = 18 
(y – 3)² + 2y² = 18 
y² – 6y + 9 + 2y² – 18 = 0 
3y² – 6y – 9 = 0 (dividir todos os membros da equação por 3) 

y² – 2y – 3 = 0 

∆ = b² – 4ac 
∆ = (–2)² – 4 * 1 * (–3) 
∆ = 4 + 12 
∆ = 16 

a = 1, b = –2 e c = –3 

Determinando os valores de x em relação aos valores de y obtidos: 

Para y = 3, temos: 

x = y – 3 
x = 3 – 3 
x = 0 

Par ordenado (0; 3) 
Para y = –1, temos: 

x = y – 3 
x = –1 –3 
x = –4 

Par ordenado (–4; –1) 

S = {(0; 3) e (–4; –1)} 

Equações irracionais

Toda equação que apresenta a variável em um radicando é considerada uma equação irracional. Observe os exemplos:

Resolvendo uma equação irracional

Ex:

1º passo: isolar o radical 

2º passo: elevar os dois membros da equação ao quadrado 

3º passo: organizar a equação 

x² - 10x +25 – x – 7 = 0
x² - 11x + 18 = 0

4º passo: resolver a equação x² - 11x + 18 = 0, aplicando o teorema de Bháskara. 

∆ = (-11)² - 4 * 1 * 18

∆ = 121 - 72

∆ = 49

x’ = (11+7)/2 = 9

x” = (11 – 7)/2 = 2

5º passo: substituir as raízes na equação original e verificar a igualdade.

x = 9

Portanto, 9 não serve.

x = 2

A única solução da equação é 2.

Por Marcos Noé

Graduado em Matemática
Equipe Brasil Escola